Maxwell’s Hypothesis:
Faraday’s Experimental Result: Suppose a conducting loop is placed in between the two poles of an electromagnet as shown in the figure below. As soon as the switch S is closed, the current in the electromagnet rises with the result that the number of magnetic flux lines passing through the loop placed in the space between the two poles of the electromagnet grows with time. If at any instant the magnetic field is B, then the magnetic flux ΦB passing through the loop of area A is given by-
| ΦB = BA |

As the magnetic field gradually establishes between the poles of the electromagnet, the magnetic flux ΦB linked with the loop increases with time. Consequently, an emf is induced in the loop which is given by ε = – dΦB/dt. This induced emf can be attributed to an electric field E induced in the coil whose value is such that-
| ε = E . 2πr = – dΦB/dt |
The induced electric field E lasts till the magnetic flux ΦB is changing. As soon as the current in the electromagnet gets established, the magnetic field B (hence ΦB) becomes steady and the induced electric field E disappears.
Result of Maxwell’s Thought Experiment: Maxwell considered a similar situation in the space between the two plates of a capacitor as shown in the figure below. As soon as the switch S is closed, a temporary charging current flows with the result that the charge q on the capacitor plates starts accumulating. The electric field E between the two plates being related to q grows with time. Since the electric flux ΦE passing through a loop of certain area A placed between the two plates of the capacitor is given by-
| ΦE = EA |
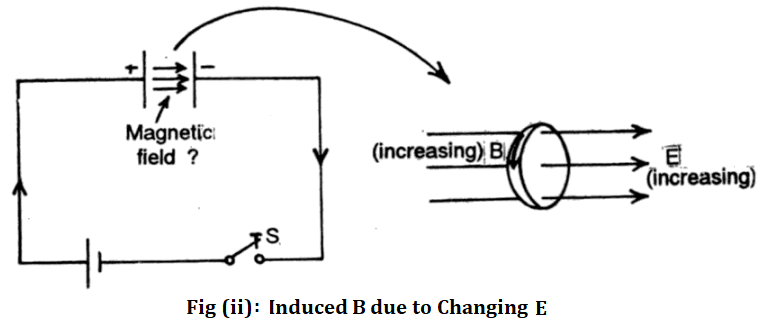
It also grows with time. Thus, during the process of charging, the electric flux ΦE passing through a loop is not constant but it varies with time.
We have seen in connection with Faraday’s experiment that when the magnetic flux ΦB passing through a loop placed in between the two poles of an electromagnet varies with time, then an electric field E is induced. In other words, a changing magnetic field induces an electric field.
Now, a question arises, “Does a changing electric flux induces a magnetic field?” This question was very carefully considered by Maxwell. He observed that during the process of charging a capacitor, (i) a temporary charging current I flow in the wires which produces a magnetic field around the wires. The magnetic field B so produced at a distance r from the wire is given by:
| B . 2πr = μ0 I ……….(i) |
This statement is known as Ampere circuital law.
There is no electric current between the two plates of the capacitor, however, instead, there is a time-varying electric flux ΦE. The question arises whether a magnetic field is induced in the space between the two plates of a capacitor during its charging.
On the basis of certain arguments, Maxwell proved that a time-varying electric field, E must induce a magnetic field B, just as time-varying B induces E. Infact, he showed that if the induced magnetic field B is represented by circular lines of force, then for a circular path of radius r fig (ii).
| B . 2πr = μ0ε0 dΦE/dt ……….(ii) |
This equation is quite similar to the equation given by Faraday, except for the negative sign. It is because of this difference, that the direction of the induced electric field (or induced current, emf) in fig (i) is opposite to the direction of the induced magnetic field in fig. (ii). Further, this equation suggests an extension of Ampere’s circuital law.
According to Maxwell, the modified version of Ampere’s circuital law is
| B . 2πr = μ0I + μ0ε0 dΦE/dt ……….(iii) |
Where I is the conduction current in the conducting wire, while ε0 dΦE/dt is the displacement current in the space between the two plates of the capacitor. In the region outside the plates of the capacitor ΦB = 0 and (iii) reduces to (i), while inside the capacitor I = 0 and (iii) reduces to (ii).








Comments (No)